Compound interest is the eighth wonder of the world. This is not financial advice and subscribe to my YouTube channel down below.
Okay, the second half wasn't true. But, compound interest is a seriously powerful formula that can make investing more lucrative than the normal cash-in-bank saving approach.
The aim of making an interest-based investment is for it to grow in value. When our investment does this, it’s called ‘simple interest’. Simple interest is what most people tend to think of when they hear the term interest.
But if we reinvest that simple interest (or just keep it invested altogether), our investment will now earn interest on the initial deposit plus the simple interest.
This means you've earned interest on your interest. And this is why we call it compound interest. So to recap, compound interest = the interest earned on your interest. Interesting…

Basic example of compound interest
Before looking into some realistic numbers, let's get the premise of compound interest down in a really basic example:
Let's take the example of Lucy.
Lucy invests £1,000 into an account that pays a compounding annual percentage rate of 3% for three years.
After year one, Lucy would earn £30 taking her investment to £1,030.
In year two, Lucy would earn 3% on £1,030, taking her total up to £1,061 (rounded up).
At the end of year three, Lucy would have £1,093 (rounded up).
By contrast, if Lucy had invested in a simple interest rate for three years, she'd have received 3% of £1,000 multiplied by three which is £1,090.
Now, in this case there is a difference of £3 between investing via simple interest vs compound interest, which isn't much. But, it becomes more powerful with two added aspects:
Time – the earlier we start, the sooner the investment grows
Money – contributing additional amounts on a regular basis (each month for example). More invested = more gained interest. As the old adage goes, money makes money.

Realistic example of compound interest
Example 1
We’ll have a look at a couple of realistic examples of compound interest now. Firstly, we’ll focus on the relationship between time and money.
This example shows how the earlier person takes advantage of compound interest when the market is returning 8%.
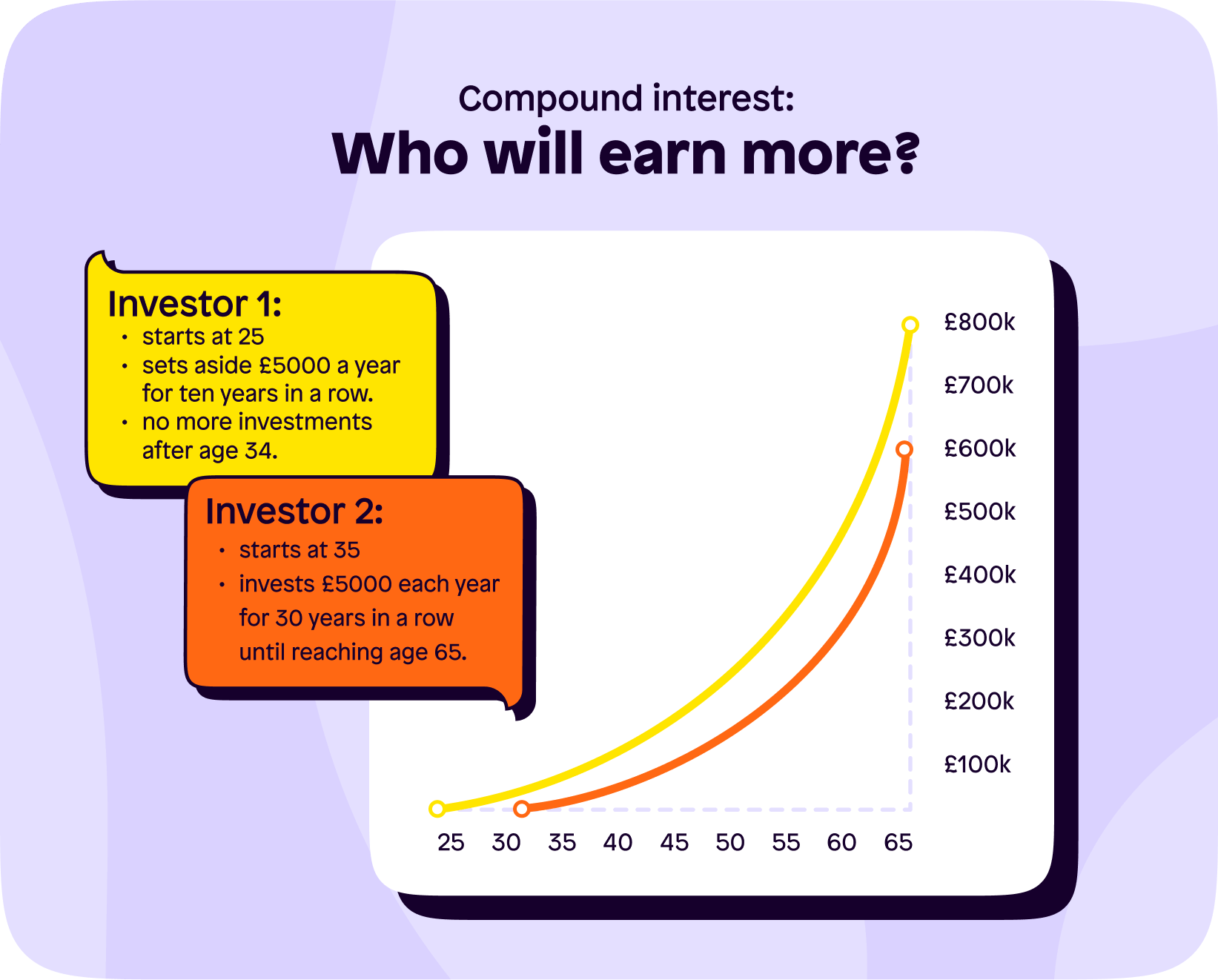
In total, investor 1 contributes £50,000 of their own money.
In total, investor 2 contributes £150,000 of their own money.
Yet, investor 1 has £176,000 more by the time they’re both 65. How is this possible?
Simple – look at when each investor started investing. Investor 1 had their investments a lot earlier meaning compound interest was already in full swing by the time investor 2 had started.
Contributing a lot of money is great, but contributing smaller amounts earlier on is just, if not more, powerful.
Example 2
Let's now look at an example of continuously compounding interest that can take place throughout someone's career.
This time, we'll be looking at Liz as an example.
Liz is keen to cut down her retirement age and makes an investment of £100 into the stock market, as this has returned 10% on average over the last century. She then continues investing £100 a month for the next 30 years.
Over the course of 30 years, she'll have invested £36,100 of her own money.
Now, let's be conservative when using the return average of the stock market and say it only returns 7% throughout those 30 years.
The total interest earned on that £36,100 is £85,287. That's over double what Liz invested herself thanks to compounding taking place. I don't know about you, but I'm starting to see what Einstein meant when he called this the eighth wonder of the world.
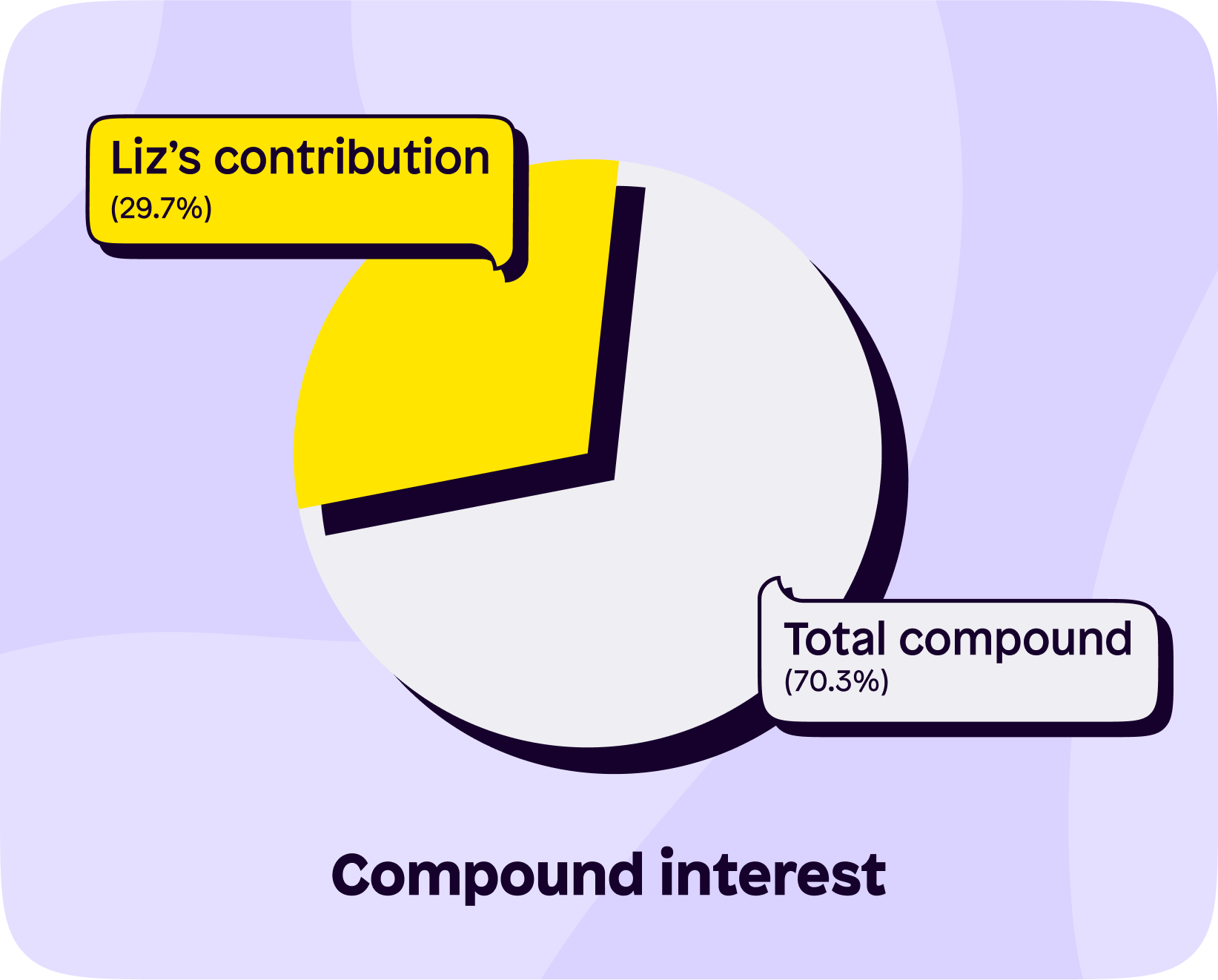
Overall, Liz's investment would be her own contributions plus the interest, which works out at £121,387. That's a 236.25% rate of return.
If you're wanting to see this in action, then down below you can see how Liz's investment looks after 10, 20 and 30 years vs just saving it without generating any form of return.
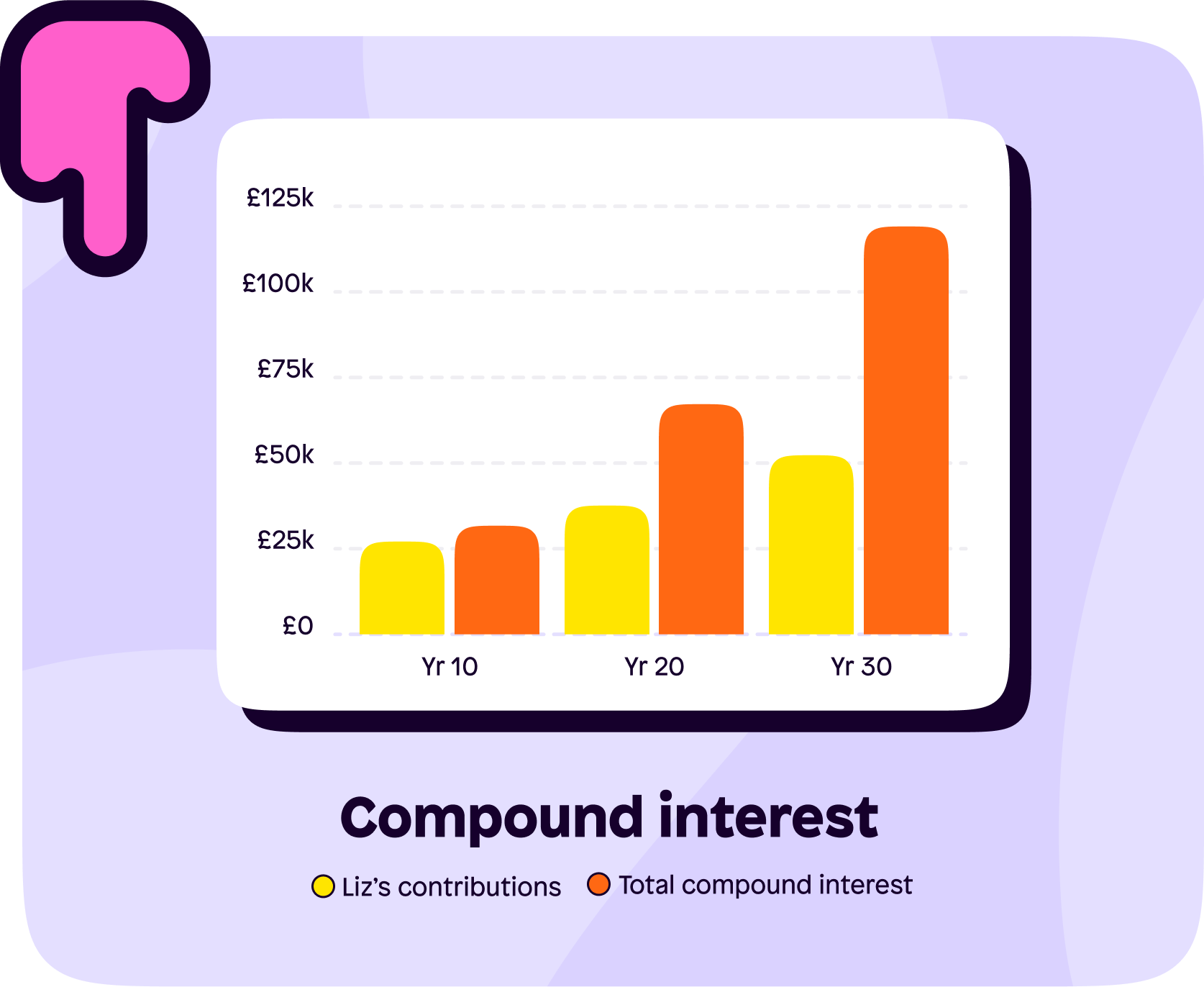
As mentioned, compound interest becomes more significant the longer it’s left invested.
Bar charts aren't for everyone though, I certainly hated them back in GCSE maths days. Here’s a pie chart to help visualise how much Liz contributed vs how much the compound interest generated.
How to work out compound interest
It's impossible to predict an exact return when calculating compound interest, but there are plenty of online calculators to help work out theoretical examples, like in Liz's example above.
We recommend using this compound interest calculator as you can alter between currencies and view the information in written columns or through different charts if you're more of a visual learner.
Becoming a millionaire
Many people view compound interest as a strong way to attain assets worth over a million by the time they retire. After playing around with the calculator above, a £1,000 investment today plus £275 a month for 35 years at a 10% annual return would be worth over £1 million.
£1,000 today plus £275 a month might sound like a lot, but that's a total contribution of £116,500, which is a heck of a lot less than £1 million.
If this is something you’re aiming for, then make sure to check out our piece on passive income – the end goal where we talk about making your investments earn you passive income around retirement age.
The rule of 72
This is a quick way to calculate how long it will take for your investment to double. It looks at how compound rates affect money. It’s a general rule and shouldn’t be treated like an exact science.
Divide 72 by your expected return of investment. Urgh, that sounded a bit jargony.
Basically, do 72 / 10 if we’re assuming the stock market returns 10% each year on our investment. (If we were to assume the stock market returned 8%, then we’d do 72 / 8.)
72 / 10 = 7.2. So, when receiving a 10% return on investment (or ROI as the pros call it) then it would take 7.2 years for our investment to double. 7.2 years might sound like a long time. But, that’s because numbers are small at the beginning.
For example, doubling £10,000 five times equals £320,000. In the first 7.2 years, the investment went from £5,000 to £10,000, but in the last 7.2 years it went from £160,000 to £320,000. Another 7.2 years would take it to £640,000.
You can see how if you start early and remain consistent, the principles of becoming a millionaire isn’t rocket science.
Compound interest and dividends

This in combination with a stock's price growing means you're benefiting from both the growth of the stock price and the dividend payments themselves. However, it is worth keeping in mind dividend stocks often have a very stable price, so the main compounding benefit typically comes from the dividend payments themselves and not the growth of the stock price.
Join us!
Ready to join the Shares community? Download the Shares app now and make sure to follow us on our socials 👇
As with all investing, your capital is at risk.
Shares is a trading name of Shares App Ltd. Shares App Ltd is an appointed representative of RiskSave Technologies Ltd, which is authorised and regulated by the Financial Conduct Authority.